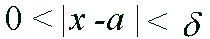Of all the concepts learned in Calculus, the one that gives way to many more ideas is that of the limit. But what is a limit? What does it mean when someone says, "the limit of 5x as x approaches 2 is 10"? The truth lies within...
THE FORMAL DEFINITION OF A LIMIT
Note that some like to refer to this concept as "The Precise Definition of a Limit"
Let's begin our journey into this monumental topic by considering the following function:
| f(x) = | 2x-1 | if | x  3 3 |
| 6 | if | x = 3 |
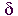 such that
such that (the Greek letter epsilon),
then we find as before that
(the Greek letter epsilon),
then we find as before that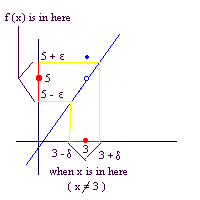
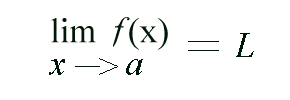
 there is a corresponding number
there is a corresponding number 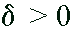 such that
such that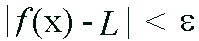 whenever
whenever